Warning
This documents an unmaintained version of NetworkX. Please upgrade to a maintained version and see the current NetworkX documentation.
communicability¶
-
communicability(G)[source]¶ Return communicability between all pairs of nodes in G.
The communicability between pairs of nodes in G is the sum of closed walks of different lengths starting at node u and ending at node v.
Parameters: G (graph) – Returns: comm – Dictionary of dictionaries keyed by nodes with communicability as the value. Return type: dictionary of dictionaries Raises: NetworkXError– If the graph is not undirected and simple.See also
communicability_centrality_exp()- Communicability centrality for each node of G using matrix exponential.
communicability_centrality()- Communicability centrality for each node in G using spectral decomposition.
communicability()- Communicability between pairs of nodes in G.
Notes
This algorithm uses a spectral decomposition of the adjacency matrix. Let G=(V,E) be a simple undirected graph. Using the connection between the powers of the adjacency matrix and the number of walks in the graph, the communicability between nodes
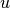 and
and  based on the graph spectrum
is [1]
based on the graph spectrum
is [1]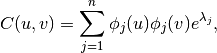
where
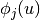 is the
is the 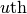 element of the
element of the 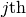 orthonormal
eigenvector of the adjacency matrix associated with the eigenvalue
orthonormal
eigenvector of the adjacency matrix associated with the eigenvalue
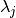 .
.References
[1] Ernesto Estrada, Naomichi Hatano, “Communicability in complex networks”, Phys. Rev. E 77, 036111 (2008). http://arxiv.org/abs/0707.0756 Examples
>>> G = nx.Graph([(0,1),(1,2),(1,5),(5,4),(2,4),(2,3),(4,3),(3,6)]) >>> c = nx.communicability(G)