Warning
This documents an unmaintained version of NetworkX. Please upgrade to a maintained version and see the current NetworkX documentation.
communicability_centrality_exp¶
-
communicability_centrality_exp(G)[source]¶ Return the communicability centrality for each node of G
Communicability centrality, also called subgraph centrality, of a node
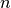 is the sum of closed walks of all lengths starting and ending at node
is the sum of closed walks of all lengths starting and ending at node 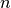 .
.Parameters: G (graph) – Returns: nodes – Dictionary of nodes with communicability centrality as the value. Return type: dictionary Raises: NetworkXError– If the graph is not undirected and simple.See also
communicability()- Communicability between all pairs of nodes in G.
communicability_centrality()- Communicability centrality for each node of G.
Notes
This version of the algorithm exponentiates the adjacency matrix. The communicability centrality of a node
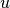 in G can be found using
the matrix exponential of the adjacency matrix of G [1] [2],
in G can be found using
the matrix exponential of the adjacency matrix of G [1] [2],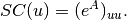
References
[1] Ernesto Estrada, Juan A. Rodriguez-Velazquez, “Subgraph centrality in complex networks”, Physical Review E 71, 056103 (2005). http://arxiv.org/abs/cond-mat/0504730 [2] Ernesto Estrada, Naomichi Hatano, “Communicability in complex networks”, Phys. Rev. E 77, 036111 (2008). http://arxiv.org/abs/0707.0756 Examples
>>> G = nx.Graph([(0,1),(1,2),(1,5),(5,4),(2,4),(2,3),(4,3),(3,6)]) >>> sc = nx.communicability_centrality_exp(G)