Warning
This documents an unmaintained version of NetworkX. Please upgrade to a maintained version and see the current NetworkX documentation.
eigenvector_centrality¶
-
eigenvector_centrality(G, max_iter=100, tol=1e-06, nstart=None, weight='weight')[source]¶ Compute the eigenvector centrality for the graph G.
Eigenvector centrality computes the centrality for a node based on the centrality of its neighbors. The eigenvector centrality for node
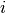 is
is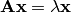
where
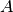 is the adjacency matrix of the graph G with eigenvalue
is the adjacency matrix of the graph G with eigenvalue 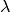 .
By virtue of the Perron–Frobenius theorem, there is a unique and positive
solution if
.
By virtue of the Perron–Frobenius theorem, there is a unique and positive
solution if 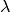 is the largest eigenvalue associated with the
eigenvector of the adjacency matrix
is the largest eigenvalue associated with the
eigenvector of the adjacency matrix 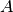 ([2]).
([2]).Parameters: - G (graph) – A networkx graph
- max_iter (integer, optional) – Maximum number of iterations in power method.
- tol (float, optional) – Error tolerance used to check convergence in power method iteration.
- nstart (dictionary, optional) – Starting value of eigenvector iteration for each node.
- weight (None or string, optional) – If None, all edge weights are considered equal. Otherwise holds the name of the edge attribute used as weight.
Returns: nodes – Dictionary of nodes with eigenvector centrality as the value.
Return type: dictionary
Examples
>>> G = nx.path_graph(4) >>> centrality = nx.eigenvector_centrality(G) >>> print(['%s %0.2f'%(node,centrality[node]) for node in centrality]) ['0 0.37', '1 0.60', '2 0.60', '3 0.37']
See also
eigenvector_centrality_numpy(),pagerank(),hits(),Notes(),------(),The(),The(),no(),iterations(),reached.(),For(),to(),first()References
[1] Phillip Bonacich: Power and Centrality: A Family of Measures. American Journal of Sociology 92(5):1170–1182, 1986 http://www.leonidzhukov.net/hse/2014/socialnetworks/papers/Bonacich-Centrality.pdf [2] Mark E. J. Newman: Networks: An Introduction. Oxford University Press, USA, 2010, pp. 169.