Warning
This documents an unmaintained version of NetworkX. Please upgrade to a maintained version and see the current NetworkX documentation.
average_clustering¶
-
average_clustering(G, nodes=None, weight=None, count_zeros=True)[source]¶ Compute the average clustering coefficient for the graph G.
The clustering coefficient for the graph is the average,
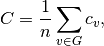
where
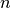 is the number of nodes in
is the number of nodes in 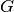 .
.Parameters: - G (graph) –
- nodes (container of nodes, optional (default=all nodes in G)) – Compute average clustering for nodes in this container.
- weight (string or None, optional (default=None)) – The edge attribute that holds the numerical value used as a weight. If None, then each edge has weight 1.
- count_zeros (bool) – If False include only the nodes with nonzero clustering in the average.
Returns: avg – Average clustering
Return type: Examples
>>> G=nx.complete_graph(5) >>> print(nx.average_clustering(G)) 1.0
Notes
This is a space saving routine; it might be faster to use the clustering function to get a list and then take the average.
Self loops are ignored.
References
[1] Generalizations of the clustering coefficient to weighted complex networks by J. Saramäki, M. Kivelä, J.-P. Onnela, K. Kaski, and J. Kertész, Physical Review E, 75 027105 (2007). http://jponnela.com/web_documents/a9.pdf [2] Marcus Kaiser, Mean clustering coefficients: the role of isolated nodes and leafs on clustering measures for small-world networks. http://arxiv.org/abs/0802.2512