Warning
This documents an unmaintained version of NetworkX. Please upgrade to a maintained version and see the current NetworkX documentation.
within_inter_cluster¶
-
within_inter_cluster(G, ebunch=None, delta=0.001, community='community')[source]¶ Compute the ratio of within- and inter-cluster common neighbors of all node pairs in ebunch.
For two nodes
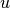 and
and  , if a common neighbor
, if a common neighbor 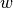 belongs to the
same community as them,
belongs to the
same community as them, 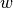 is considered as within-cluster common
neighbor of
is considered as within-cluster common
neighbor of 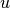 and
and  . Otherwise, it is considered as
inter-cluster common neighbor of
. Otherwise, it is considered as
inter-cluster common neighbor of 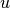 and
and  . The ratio between the
size of the set of within- and inter-cluster common neighbors is
defined as the WIC measure. [1]
. The ratio between the
size of the set of within- and inter-cluster common neighbors is
defined as the WIC measure. [1]Parameters: - G (graph) – A NetworkX undirected graph.
- ebunch (iterable of node pairs, optional (default = None)) – The WIC measure will be computed for each pair of nodes given in the iterable. The pairs must be given as 2-tuples (u, v) where u and v are nodes in the graph. If ebunch is None then all non-existent edges in the graph will be used. Default value: None.
- delta (float, optional (default = 0.001)) – Value to prevent division by zero in case there is no inter-cluster common neighbor between two nodes. See [1] for details. Default value: 0.001.
- community (string, optional (default = ‘community’)) – Nodes attribute name containing the community information. G[u][community] identifies which community u belongs to. Each node belongs to at most one community. Default value: ‘community’.
Returns: piter – An iterator of 3-tuples in the form (u, v, p) where (u, v) is a pair of nodes and p is their WIC measure.
Return type: iterator
Examples
>>> import networkx as nx >>> G = nx.Graph() >>> G.add_edges_from([(0, 1), (0, 2), (0, 3), (1, 4), (2, 4), (3, 4)]) >>> G.node[0]['community'] = 0 >>> G.node[1]['community'] = 1 >>> G.node[2]['community'] = 0 >>> G.node[3]['community'] = 0 >>> G.node[4]['community'] = 0 >>> preds = nx.within_inter_cluster(G, [(0, 4)]) >>> for u, v, p in preds: ... '(%d, %d) -> %.8f' % (u, v, p) ... '(0, 4) -> 1.99800200' >>> preds = nx.within_inter_cluster(G, [(0, 4)], delta=0.5) >>> for u, v, p in preds: ... '(%d, %d) -> %.8f' % (u, v, p) ... '(0, 4) -> 1.33333333'
References
[1] (1, 2) Jorge Carlos Valverde-Rebaza and Alneu de Andrade Lopes. Link prediction in complex networks based on cluster information. In Proceedings of the 21st Brazilian conference on Advances in Artificial Intelligence (SBIA‘12) http://dx.doi.org/10.1007/978-3-642-34459-6_10