Warning
This documents an unmaintained version of NetworkX. Please upgrade to a maintained version and see the current NetworkX documentation.
quotient_graph¶
-
quotient_graph(G, node_relation, edge_relation=None, create_using=None)[source]¶ Returns the quotient graph of
Gunder the specified equivalence relation on nodes.Parameters: - G (NetworkX graph) – The graph for which to return the quotient graph with the specified node relation.
- node_relation (Boolean function with two arguments) – This function must represent an equivalence relation on the nodes of
G. It must take two arguments u and v and returnTrueexactly when u and v are in the same equivalence class. The equivalence classes form the nodes in the returned graph. - edge_relation (Boolean function with two arguments) –
This function must represent an edge relation on the blocks of
Gin the partition induced bynode_relation. It must take two arguments, B and C, each one a set of nodes, and returnTrueexactly when there should be an edge joining block B to block C in the returned graph.If
edge_relationis not specified, it is assumed to be the following relation. Block B is related to block C if and only if some node in B is adjacent to some node in C, according to the edge set ofG. - create_using (NetworkX graph) – If specified, this must be an instance of a NetworkX graph class. The nodes and edges of the quotient graph will be added to this graph and returned. If not specified, the returned graph will have the same type as the input graph.
Returns: The quotient graph of
Gunder the equivalence relation specified bynode_relation.Return type: NetworkX graph
Examples
The quotient graph of the complete bipartite graph under the “same neighbors” equivalence relation is
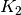 . Under this relation, two nodes
are equivalent if they are not adjacent but have the same neighbor set:
. Under this relation, two nodes
are equivalent if they are not adjacent but have the same neighbor set:>>> import networkx as nx >>> G = nx.complete_bipartite_graph(2, 3) >>> same_neighbors = lambda u, v: (u not in G[v] and v not in G[u] ... and G[u] == G[v]) >>> Q = nx.quotient_graph(G, same_neighbors) >>> K2 = nx.complete_graph(2) >>> nx.is_isomorphic(Q, K2) True
The quotient graph of a directed graph under the “same strongly connected component” equivalence relation is the condensation of the graph (see
condensation()). This example comes from the Wikipedia article `Strongly connected component`_:>>> import networkx as nx >>> G = nx.DiGraph() >>> edges = ['ab', 'be', 'bf', 'bc', 'cg', 'cd', 'dc', 'dh', 'ea', ... 'ef', 'fg', 'gf', 'hd', 'hf'] >>> G.add_edges_from(tuple(x) for x in edges) >>> components = list(nx.strongly_connected_components(G)) >>> sorted(sorted(component) for component in components) [['a', 'b', 'e'], ['c', 'd', 'h'], ['f', 'g']] >>> >>> C = nx.condensation(G, components) >>> component_of = C.graph['mapping'] >>> same_component = lambda u, v: component_of[u] == component_of[v] >>> Q = nx.quotient_graph(G, same_component) >>> nx.is_isomorphic(C, Q) True
Node identification can be represented as the quotient of a graph under the equivalence relation that places the two nodes in one block and each other node in its own singleton block:
>>> import networkx as nx >>> K24 = nx.complete_bipartite_graph(2, 4) >>> K34 = nx.complete_bipartite_graph(3, 4) >>> C = nx.contracted_nodes(K34, 1, 2) >>> nodes = {1, 2} >>> is_contracted = lambda u, v: u in nodes and v in nodes >>> Q = nx.quotient_graph(K34, is_contracted) >>> nx.is_isomorphic(Q, C) True >>> nx.is_isomorphic(Q, K24) True