Warning
This documents an unmaintained version of NetworkX. Please upgrade to a maintained version and see the current NetworkX documentation.
power¶
-
power(G, k)[source]¶ Returns the specified power of a graph.
The
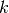 -th power of a simple graph
-th power of a simple graph 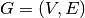 is the graph
is the graph
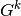 whose vertex set is
whose vertex set is 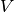 , two distinct vertices
, two distinct vertices 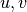 are
adjacent in
are
adjacent in 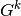 if and only if the shortest path
distance between
if and only if the shortest path
distance between 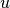 and
and  in
in 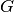 is at most
is at most 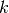 .
.Parameters: - G (graph) – A NetworkX simple graph object.
- k (positive integer) – The power to which to raise the graph
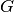 .
.
Returns: 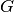 to the
to the 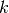 -th power.
-th power.Return type: NetworkX simple graph
Raises: - exc:
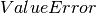 –
If the exponent
–
If the exponent 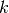 is not positive.
is not positive. NetworkXError– If G is not a simple graph.
Examples
>>> G = nx.path_graph(4) >>> nx.power(G,2).edges() [(0, 1), (0, 2), (1, 2), (1, 3), (2, 3)] >>> nx.power(G,3).edges() [(0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 3)]
A complete graph of order n is returned if k is greater than equal to n/2 for a cycle graph of even order n, and if k is greater than equal to (n-1)/2 for a cycle graph of odd order.
>>> G = nx.cycle_graph(5) >>> nx.power(G,2).edges() == nx.complete_graph(5).edges() True >>> G = nx.cycle_graph(8) >>> nx.power(G,4).edges() == nx.complete_graph(8).edges() True
References
[1] - Bondy, U. S. R. Murty, Graph Theory. Springer, 2008.
Notes
Exercise 3.1.6 of Graph Theory by J. A. Bondy and U. S. R. Murty [1].