Warning
This documents an unmaintained version of NetworkX. Please upgrade to a maintained version and see the current NetworkX documentation.
communicability_betweenness_centrality¶
-
communicability_betweenness_centrality(G, normalized=True)[source]¶ Return communicability betweenness for all pairs of nodes in G.
Communicability betweenness measure makes use of the number of walks connecting every pair of nodes as the basis of a betweenness centrality measure.
Parameters: G (graph) – Returns: nodes – Dictionary of nodes with communicability betweenness as the value. Return type: dictionary Raises: NetworkXError– If the graph is not undirected and simple.See also
communicability()- Communicability between all pairs of nodes in G.
communicability_centrality()- Communicability centrality for each node of G using matrix exponential.
communicability_centrality_exp()- Communicability centrality for each node in G using spectral decomposition.
Notes
Let
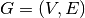 be a simple undirected graph with
be a simple undirected graph with 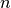 nodes and
nodes and 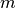 edges,
and
edges,
and 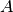 denote the adjacency matrix of
denote the adjacency matrix of 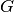 .
.Let
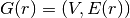 be the graph resulting from
removing all edges connected to node
be the graph resulting from
removing all edges connected to node  but not the node itself.
but not the node itself.The adjacency matrix for
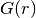 is
is 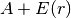 , where
, where 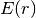 has nonzeros
only in row and column
has nonzeros
only in row and column  .
.The communicability betweenness of a node
 is [1]
is [1]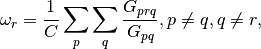
where
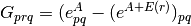 is the number of walks
involving node r,
is the number of walks
involving node r,
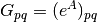 is the number of closed walks starting
at node
is the number of closed walks starting
at node 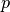 and ending at node
and ending at node 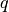 ,
and
,
and 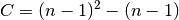 is a normalization factor equal to the
number of terms in the sum.
is a normalization factor equal to the
number of terms in the sum.The resulting
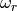 takes values between zero and one.
The lower bound cannot be attained for a connected
graph, and the upper bound is attained in the star graph.
takes values between zero and one.
The lower bound cannot be attained for a connected
graph, and the upper bound is attained in the star graph.References
[1] Ernesto Estrada, Desmond J. Higham, Naomichi Hatano, “Communicability Betweenness in Complex Networks” Physica A 388 (2009) 764-774. http://arxiv.org/abs/0905.4102 Examples
>>> G = nx.Graph([(0,1),(1,2),(1,5),(5,4),(2,4),(2,3),(4,3),(3,6)]) >>> cbc = nx.communicability_betweenness_centrality(G)